Câu hỏi:
12/07/2024 7,466
Trả lời:
![]()
Giải vì chưng Vietjack
a) Ta có:
(P) trải qua những điểm sở hữu tọa chừng như bảng sau:
|
x |
–2 |
–1 |
1 |
2 |
|
|
y = x2 |
4 |
1 |
1 |
4 |
Đỉnh của (P) là O(0;0)
(d) trải qua những điểm sở hữu tọa chừng (0;2), (2;0)
Ta sở hữu đồ vật thị như sau:
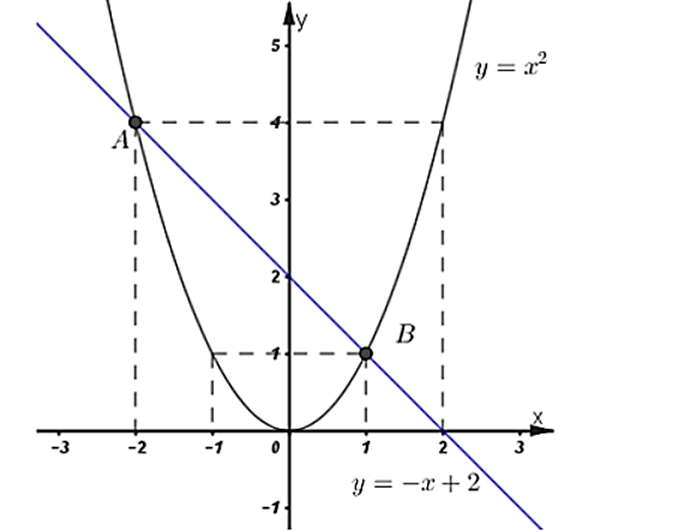
b) Xét phương trình hoành chừng giao phó điểm:
x2 = –x + 2
⇔ x2 + x – 2 = 0
⇔ x2 + 2x – x – 2 = 0
⇔ x(x + 2) – (x + 2) = 0
⇔ (x + 2)(x – 1) = 0
⇔ \(\left[ \begin{array}{l}x = - 2\\x = 1\end{array} \right.\)
⇒ \(\left[ \begin{array}{l}y = 4\\y = 1\end{array} \right.\)
Vậy nhì đồ vật thị hạn chế nhau bên trên nhì điểm phân biệt A(−2; 4) và B(1; 1).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Trong một kì đua sở hữu 60% sỹ tử đua đỗ. Hai chúng ta A và B nằm trong tham gia dự thi tê liệt. Xác suất nhằm chỉ có một chúng ta đua đỗ?
Câu 2:
Trong mặt mày phẳng lì, mang lại tam giác ABC sở hữu AC = 4 centimet, \(\widehat A\)= 60°, \(\widehat B\)= 45°. Độ lâu năm cạnh BC là?
Câu 3:
Một xe hơi dự tính chuồn kể từ A cho tới B vô một thời hạn chắc chắn. Nếu xe đua với véc tơ vận tốc tức thời 35km/h thì cho tới điểm chậm trễ thất lạc 2 tiếng đồng hồ. Nếu xe đua với véc tơ vận tốc tức thời 50km/h thì cho tới điểm sớm rộng lớn 1 giờ. Tìm quãng đàng AB và thời hạn dự tính chuồn khi đầu.
Câu 4:
Cho tứ diện ABCD. Gọi I, J theo thứ tự là trung điểm của BC, BD. (P) là mp qua quýt IJ và hạn chế AC, AD theo thứ tự bên trên N, M. Chứng minh tứ giác IJMN là hình thang. Nếu M là trung điểm AD thì tứ giác IJMN là hình gì?
Câu 5:
Tìm số hạng trước tiên của cấp cho số nhân, hiểu được công bội là 3, tổng những số hạng là 728 và số hạng cuối là 486.
Câu 6:
Cho hình bình hành ABCD: AB = 2 , AD = 1, \(\widehat {BAD} = 60^\circ \). Tính \(\overrightarrow {AB} .\overrightarrow {AD} \).
Câu 7:
Cho tam giác ABC (AB < AC) sở hữu phụ thân góc nhọn nội tiếp vô đàng tròn trĩnh tâm O, nửa đường kính R. Gọi H là giao phó điểm của phụ thân đàng cao AD, BE, CF của tam giác ABC.
a) Chứng minh rằng AEHF và AEDB là những tứ giác nội tiếp đàng tròn trĩnh.
b) Vẽ 2 lần bán kính AK của đàng tròn trĩnh (O). Chứng minh tam giác ABD và tam giác AKC đồng dạng cùng nhau. Suy rời khỏi AB.AC = 2R.AD.
c) Chứng minh OC vuông góc với DE.
Cho tam giác ABC (AB < AC) sở hữu phụ thân góc nhọn nội tiếp vô đàng tròn trĩnh tâm O, nửa đường kính R. Gọi H là giao phó điểm của phụ thân đàng cao AD, BE, CF của tam giác ABC.
a) Chứng minh rằng AEHF và AEDB là những tứ giác nội tiếp đàng tròn trĩnh.
b) Vẽ 2 lần bán kính AK của đàng tròn trĩnh (O). Chứng minh tam giác ABD và tam giác AKC đồng dạng cùng nhau. Suy rời khỏi AB.AC = 2R.AD.
c) Chứng minh OC vuông góc với DE.
Bình luận
Hãy Đăng nhập hoặc Tạo thông tin tài khoản nhằm gửi comment
Bình luận
🔥 Đề đua HOT:
