Câu hỏi:
13/07/2024 40,237
Cho ∆ABC với AB = 2, AC = 3, \(\widehat A = 60^\circ \). Tính phỏng nhiều năm phân giác \(\widehat A\).
Trả lời:
![]()
Giải tự Vietjack
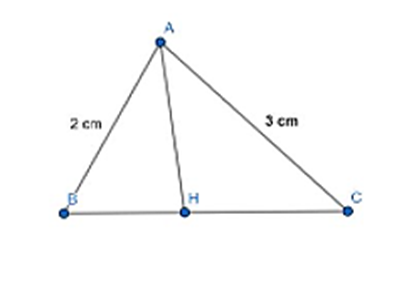
Áp dụng ấn định lí hàm số côsin cho tới ∆ABC tớ có: \(B{C^2} = A{B^2} + A{C^2} - 2AB.AC.cos60^\circ = \sqrt 7 \)
Gọi AH là đàng phân giác góc A.
Áp dụng đặc điểm đàng phân giác cho tới ∆ABC: \(\frac{{AB}}{{AC}} = \frac{{BH}}{{HC}}\)
\(\frac{{AB}}{{BH}} = \frac{{AC}}{{HC}} = \frac{{AB + AC}}{{BH + HC}} = \frac{{2 + 3}}{{BC}} = \frac{5}{{\sqrt 7 }}\)
\( \Rightarrow BH = AB:\frac{5}{{\sqrt 7 }} = \frac{{2\sqrt 7 }}{5}\)
\(\cos \widehat B = \frac{{A{C^2} - A{B^2} - B{C^2}}}{{ - 2AB.BC}} = \frac{{\sqrt 7 }}{{14}}\)
Xét ∆ABH có: \(A{H^2} = A{B^2} + B{H^2} - 2.AB.BH.cos\widehat B = \frac{{108}}{{25}} \Rightarrow AH = \frac{{6\sqrt 3 }}{5}\).
Nhà sách VIETJACK:
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Câu 1:
Cho \(\cos x = \frac{2}{{\sqrt 5 }},0 < x < \frac{\pi }{2}\). Tính những độ quý hiếm lượng giác của góc x.
Câu 2:
Cho ∆ABC với \(\frac{5}{{\sin A}} = \frac{4}{{\sin B}} = \frac{3}{{\sin C}}\) và a = 10. Tính chu vi tam giác.
Câu 3:
Cho tana = 2. Tính độ quý hiếm của biểu thức \(C = \frac{{\sin a}}{{{{\sin }^3}a + 2{{\cos }^3}a}}\).
Câu 4:
Trên khoảng tầm \(\left( {\frac{\pi }{2};2\pi } \right)\), phương trình \(\cos \left( {\frac{\pi }{6} - 2\pi } \right) = \sin x\) với từng nào nghiệm ?
Câu 5:
Cho ∆ABC. Gọi M, N, Phường thứu tự là trung điểm những cạnh AB, AC, BC. Hỏi \(\overrightarrow {MP} + \overrightarrow {NP} \) tự vectơ nào?
Câu 6:
Cho hình bình hành ABCD. E, F thứu tự là trung điểm của AB và CD.
a. Tứ giác DEBF là hình gì? Vì sao?
b. Chứng minh 3 đường thẳng liền mạch AC, BD, EF đồng quy.
c. Gọi giao phó điểm của AC với DE và BF theo dõi trật tự là M, N. Chứng minh tứ giác EMFN là hình bình hành.
Cho hình bình hành ABCD. E, F thứu tự là trung điểm của AB và CD.
a. Tứ giác DEBF là hình gì? Vì sao?
b. Chứng minh 3 đường thẳng liền mạch AC, BD, EF đồng quy.
c. Gọi giao phó điểm của AC với DE và BF theo dõi trật tự là M, N. Chứng minh tứ giác EMFN là hình bình hành.
Bình luận
Hãy Đăng nhập hoặc Tạo thông tin tài khoản nhằm gửi comment
Bình luận
