Tìm tâm đối xứng của đồ thị hàm số y=(2x+1)/(x-3) (Miễn phí)

B.\(B\left( { - 3;2} \right).\)

C.\(D\left( { - 1;3} \right).\)

D. \(C\left( {1; - 3} \right).\)

Trả lời:

Ta có: \(\mathop {\lim }\limits_{x \to \pm \infty } hắn = 2 \Rightarrow \) đường thẳng liền mạch \(y = 2\)là tiệm cận ngang của đồ gia dụng thị hàm số.

\(\mathop {\lim }\limits_{x \to {3^ + }} hắn = + \infty ;\mathop {\lim }\limits_{x \to {3^ - }} hắn = - \infty \Rightarrow \) đường thẳng liền mạch \(x = 3\) là tiệm cận đứng của đồ gia dụng thị hàm số.

Vậy tâm đối xứng của đồ gia dụng thị là \(A\left( {3;2} \right).\)

Đáp án A

Tìm \(m\) nhằm hàm số \(y = \frac{1}{3}{x^3} - m{x^2} + \left( {{m^2} - 4} \right)x + 3\) đạt cực to bên trên điểm x=3.

A.\(m = - 1.\)

B. \(m = 1.\)

C.\(m = 5.\)

D. \(m = - 5.\)

Có từng nào độ quý hiếm nguyên vẹn của thông số \(m\) nằm trong đoạn \(\left[ { - 20;2} \right]\) nhằm hàm số $y=x^3-x^2+3mx-1$ đồng vươn lên là bên trên \(\mathbb{R}.\) 

A. 2.

B.23.

C.20.

D. 3.

Cho lăng trụ đứng \(ABC.A'B'C'\) có tính lâu năm cạnh mặt mày là \(2a,\) lòng \(ABC\) là tam giác vuông cân nặng bên trên \(A,\) góc thân thiện \(AC'\) và mặt mày bằng \(\left( {BCC'B'} \right)\) vì như thế \({30^0}\) (tham khảo hình vẽ).

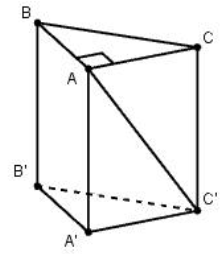
Tính theo đuổi \(a\) thể tích khối trụ đem nhị lòng là hai tuyến đường tròn trặn nước ngoài tiếp nhị lòng của lăng trụ \(ABC.A'B'C'.\) 

A.\(\pi {a^3}.\)

B. \(3\pi {a^3}.\)

C.\(2\pi {a^3}.\) 

D.\(4\pi {a^3}.\)

Cho nhị số thực dương \(a,b.\) Rút gọn gàng biểu thức \[\] tao nhận được \(A = {a^m}.{b^n}.\)

A.\(\frac{1}{{21}}.\) 

B.\(\frac{1}{9}.\)

C.\(\frac{1}{{18}}.\)

D. \(\frac{1}{8}.\)

Viết phương trình tiếp tuyến của đồ gia dụng thị hàm số \(y = \frac{{2x - 1}}{{x - 2}},\) biết tiếp tuyến đem thông số góc \(k = - 3\) 

A.\(y = - 3x + 4.\)

B.\(y = - 3x + 14\) và \(y = - 3x + 2.\)

C.\(y = - 3x - 14\) và \(y = - 3x - 2.\)

D.\(y = - 3x - 14.\)

Cho hình lăng trụ đứng \(ABC.A'B'C'\) đem lòng \(ABC\) vuông bên trên \(A,AB = a,BC = 2a,\) mặt mày mặt \(ACC'A'\) là hình vuông vắn. Gọi \(M,N,P\) thứu tự là trung điểm của \(AC,CC',A'B'\) và \(H\) là hình chiếu của \(A\) lên \(BC.\) Tính theo đuổi \(a\) khoảng cách thân thiện hai tuyến đường trực tiếp \(MP\) và \(HN.\)

A.\(\frac{{a\sqrt 3 }}{4}.\)

B.\(\frac{{a\sqrt 3 }}{2}.\)

C.\(a\sqrt 3 .\)

D. \(\frac{a}{4}.\)

Hãy Đăng nhập hoặc Tạo thông tin tài khoản nhằm gửi phản hồi

Bình luận